All about Game Theory
Game theory is the science of decision making. It is a process of modeling strategic interaction between individuals set in a situation bound by a set of rules and possible outcomes. It is widely applied in various fields including economics, politics, military tactics, business decisions, etc. This PenMyPaper article can help you do your university paper without any hassle. This article can help you do my university paper without any hassle. Keep in mind that game theory does not involve game as we traditionally know them to be. In this theory a game can be defined as:
‘Any interaction between two or more people, in which the payoff of each person is affected by the decisions made by others’
Game theory can be applied to any decisions that you have made in a social interaction, in any perceivable context, such as deciding on breaking the cab fare with friends or asking your tutor for essay help. In order to understand game theory better let us look at some of the key definitions:
A Player: A player is any strategic decision maker in context of the game. It can be an individual or even an organization or an institution.
A Strategy: A strategy is a plan of action taken by a player while considering the given set of conditions.
The Payoff: The payoff is the outcome of a chosen strategy by a player.
Optimal Strategy: The strategy which offers the maximum payoff.
The objective of game theory is to help players make decisions which can lead to maximum payoff.
Let's Dig Deeper into Game Theory
Having a comprehensive understanding of Game Theory can be extremely beneficial for a management student. However, if you're struggling with the topic, say game theory between Samsung vs Apple competitors, you can simply ask our experts to produce a high-quality paper for you. In game theory, the games can be fundamentally segregated into two different types, which are:
- Non-Cooperative Game
- Cooperative Game
Non-Cooperative Game Theory
A non-cooperative game is the one which models conflicting situations, where there can be some winners and some losers. In this game, the payoff received by one player is dependent on his or her own decisions, and also on the decisions made by the other players. In this case the players seek to take the most rational strategy. The most common example of non-cooperative game theory is Prisoner’s Dilemma, which is a hypothetical game.
In Prisoner’s Dilemma, 2 criminals have been arrested for robbery and are held in two separate interrogation rooms, where they cannot communicate with each other. Even though the police are absolutely certain about their crime, they do not have enough evidence, so they need them to confess. So the law enforcement wants to cut them a deal and here’s how it goes: If none of them confess, both will have to spend 2 years in jail. If both of them confess, then both of them will have to go to jail for 4 years. However, if one of them confesses and exposes the other one, the confessor will be set free and the other person will get jail time for 8 years. Let us look at these conditions in a matrix:
| Prisoner 1 Doesn’t Confess | Prisoner 1 Confesses | |
|---|---|---|
| Prisoner 2 Doesn’t Confess | Both get 2 years jail time | Prisoner 2 gets 8 years jail time; Prisoner 1 gets free |
| Prisoner 2 Confesses | Prisoner 1 gets 8 years jail time; Prisoner 2 gets free | Both gets 4 years of jail time |
Based on the conditions, the most favorable outcome for both of them is to not confess; so that both get minimum (2 years) jail time. However, even though this is the best bet for both of them, none of them have any reason to trust each other. Prisoner 1 cannot be sure that Prisoner 2 will keep his mouth shut, and same goes for Prisoner 2. Any of the two prisoners doesn’t want to take the risk of getting 8 years of jail time, if one of them doesn’t confess and the other does. In this case, the payoff where both get 4 years of jail time, has the least amount of risk. This particular outcome is what is called Nash Equilibrium.
‘A player has found them self in Nash Equilibrium, if their choices lead to the maximum available payoff, irrespective of what the others decide.’
In case of the Prisoner’s Dilemma, both of them is equally better off with the decision of confessing, no matter what the other person decides to do. If a person confesses, he doesn’t have to worry about what the other person has done, and will only get the maximum of 4 years of prison, without taking the risk of getting 8 years, by not confessing. However, the payoff where both get 2 years of jail time is an unstable state, because its occurrence is dependent on the decision of the other person. You can use prisoner’s dilemma as a compelling critical thinking college essay for explaining non-cooperative game theory.
Thus, in non-cooperative game theory, the players aim to choose the course of action which leads to Nash Equilibrium, where the player benefits the most, regardless of what the other decides to do.
Cooperative Game Theory
In a cooperative game, all the players in achieve a best joint outcome. In this case, all the players agree to work together to form a coalition or alliance and to proceed towards a common goal of the best possible payoff. As opposed to non-cooperative game theory, the players will not compete against each other and each of them will act in order to reach the best possible goal. It is important to understand that in cooperative game, the formation of a coalition prevents players to act in a competitive manner.
Just like players in a non-cooperative game seeks to achieve the Nash Equilibrium, the players in a cooperative game aims at achieving the Shapley Value. The Shapley Value can be described as:
‘The process of dividing the payoff among the players based on the value of individual contribution.’
The objective of Shapley value is to offer fair distribution of the benefits to each member of the coalition or alliance based on their respective contribution. It is based on the belief that players should receive benefits which is justified and fair for them. Thus, if a player has invested most resources and effort in the coalition, then he will get the most payoff, on the other hand the player who has contributed minimum effort and resources, should get minimum payoff.
The Shapley Value is determined by the formula:
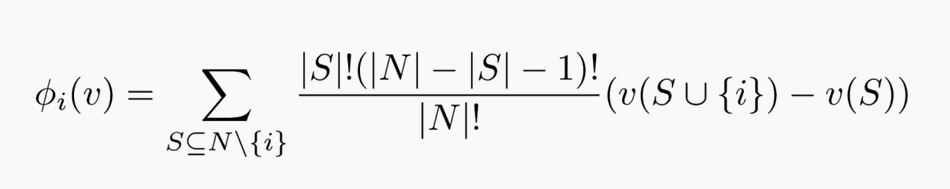
The Shapley Value is based on certain axioms or principles, that the member of the coalition must follow, which are:
- The contribution of a player is determined by calculating the payoff, by eliminating from the game itself, which is known as Marginal Contribution.
- Players with same contribution to the coalition have equal value.
- Player with no contribution should receive nothing. (In certain cases the coalition may decide to provide a player with no contribution with some benefits)
- The varying costs or contributions of different parts of a game should be broken down within the respective parts.
Thus, if the distribution of the payoff in a coalition satisfies all the axioms, then it has followed the Shapley Value.
For the sake of a much simpler explanation, let us discuss itwithout the formula and with help of a hypothetical scenario, which satisfies the axioms.
Let us assume that two friends Bob and Alex have decided to make and sell cupcakes. However, Bob and Alex work with different efficiencies and resource contribution, where Bob can make 10 cupcakes when working alone and Alex can make 20 cupcakes when working alone. But when working together, the operation becomes more optimized and together they can make 40 cupcakes. Selling each of them for a dollar, gives them $40.

Now the question arises: how should Bob and Alex divide their share? Should they divide equally? But that will not be fair, because the marginal contribution of Alex is more than that of Bob, so according to Shapley Value their payoff should be based on their contribution.
Marginal Contribution of Alex to Bob= 40 – 10= 30 Cupcakes
Marginal Contribution of Bob to Alex = 40 – 20 =20 Cupcakes
Thus, Bob alone can make 10 cupcakes, but together his contribution is 20 cupcakes. Based on the Shapley Value, these two contributions should be averaged. Thus the contribution of Bob is (10+20)/2 = 15 cupcakes and should receive the payoff for these 15 only, which is $15, whereas Alex should get $40 - $15 = $25.
Thus, Bob gets $15 and Alex gets $25.
This is a much simpler explanation of Shapley Value and how it can be used to distribute payoffs in a coalition. In real life situations, the same approach can be used to find out the marginal value of each player to each other and averaging them to find out their payoff.
What Have We Learnt About Game Theory
As you search through a pool of debatable topics to finally choose a prompt befitting your expertise and assignment requirements, the same way game theory can help in making the right decision in any given scenario where you interact with other players. In case of the non-cooperative game theory, it helps in making the smartest decision, which offers maximum possible gain or payoff, at minimum possible risk.On the other hand, the cooperative game theory helps in being most fair in distribution of payoff, within a coalition or alliance.Thus, game theory can be used in almost every situation that involves any form of decision making, whether it be two parties negotiating on a price or the world leaders discussing on the use of renewable energy.
Need Expert Help with Game Theory?
Like of learning about strategic alliances, Game Theory can be quite a complex task to master, especially if you haven’t been well conversant with it. But, that should not stop you from getting good grades in your papers. Avail our help with essays and let our experts deal with your game theory problems or any other academic problems for that matter.

